非饱和带内流固吸附作用介观物理模型: 薄膜水对土壤持水性能、渗透性能和湿度分布的影响
摘要:
地下水是全球水文循环系统的重要组成部分,含水层和包气带的土壤水力特性是水文地质领域中的核心议题之一。当前建立的基于粘性力主导的达西定律和基于毛细力主导的基质吸力曲线,对于颗粒表面流-固吸附作用不可忽略的低渗透性土壤会产生较大误差。由于颗粒表面的范德华引力、静电引力、水合作用力等吸附作用,饱和带颗粒表面会形成非牛顿流体边界层,呈现启动水力梯度等非达西流现象;非饱和带颗粒表面会形成薄膜水,传统持水函数在超高基质吸力范围不能较好地拟合测量结果。 本项目将在格子Boltzmann模型框架下进行介观尺度建模,构建连续且随着距离衰减的流-固粘附作用力,将其引入简单几何形状孔隙和低渗透性多孔介质的单相流和两相流中。并结合微流控实验验证、孔隙尺度分析与升维分析等研究方法,阐释颗粒表面边界层和薄膜水的形成过程。计算单相流中边界层的密度和粘度分布、滑移长度和流量提高比,结合孔隙形状与尺寸分布阐释多孔介质非达西流效应的物理机制。计算两相流中薄膜水厚度、水-气界面曲率和欧拉长度,阐释多孔介质在中低含水量时超高基质吸力的物理机制。本项目的研究成果将有助于深刻理解低渗透性地下水系统流-固界面物理过程与土壤水力特性之间的关系。
内容:
本项目开展的工作内容包括:在多相格子Boltzmann方法框架下,建立多孔介质中饱和流和非饱和流的连续且指数衰减流固粘附力介观物理模型。(a)模拟薄膜水在饱和流中固体表面的生成过程、密度分布和导致的滑移流效应(即非达西流效应)(Li et al, Phys. Rev. Fluids, 2021);(b)模拟薄膜水在非饱和流中颗粒表面的生成过程、孔隙尺度流体分布和其对持水曲线形状的影响(Li et al, Adv. Water Resour, 2025)。
(a1)根据表面力测量实验的发现(有滑移流和无滑移流的固体表面之间的表面力之差即等于流-固粘附力大小;正是流-固粘附力造成了固体表面的滑移现象)(Baudry et al.,Langmuir,2001;Craig et al., Phys. Rev. Lett,2001)和前人提出的固体表面之间的指数衰减型表面力函数(Vinogradova,Langmuir,1998;Vinogradova,Int. J. Miner. Process,1999),本工作构建了的流体粒子与固体墙之间的连续且指数衰减的流-固粘附力模型,推导出了平行平板微通道内密度分布、流速分布、滑移长度和流量提高比关于粘附作用强度、衰减长度与通道间隙的解析解。该解析解成功地应用于两组经典的滑移流微流控物理实验中(Tretheway and Meinhart,Phys. Fluids,2002;Joseph and Tabeling,Phys. Rev. E,2005)(两组实验均采用微米粒子图像测速仪测量通道间隙内的流速分布,通道间隙宽度的尺度数量级为10微米;第一组实验通道表面材料为Glass-Glass和OTS-OTS,滑移长度数量级为1微米,图1a;第二组实验通道表面材料为Glass-PDMS和OTS-PDMS,滑移长度数量级为10纳米,图1b),率定了流-固粘附作用强度、衰减长度等参数,该参数可以应用于相同材料却不同间隙宽度的平行平板微通道滑移流模拟中。
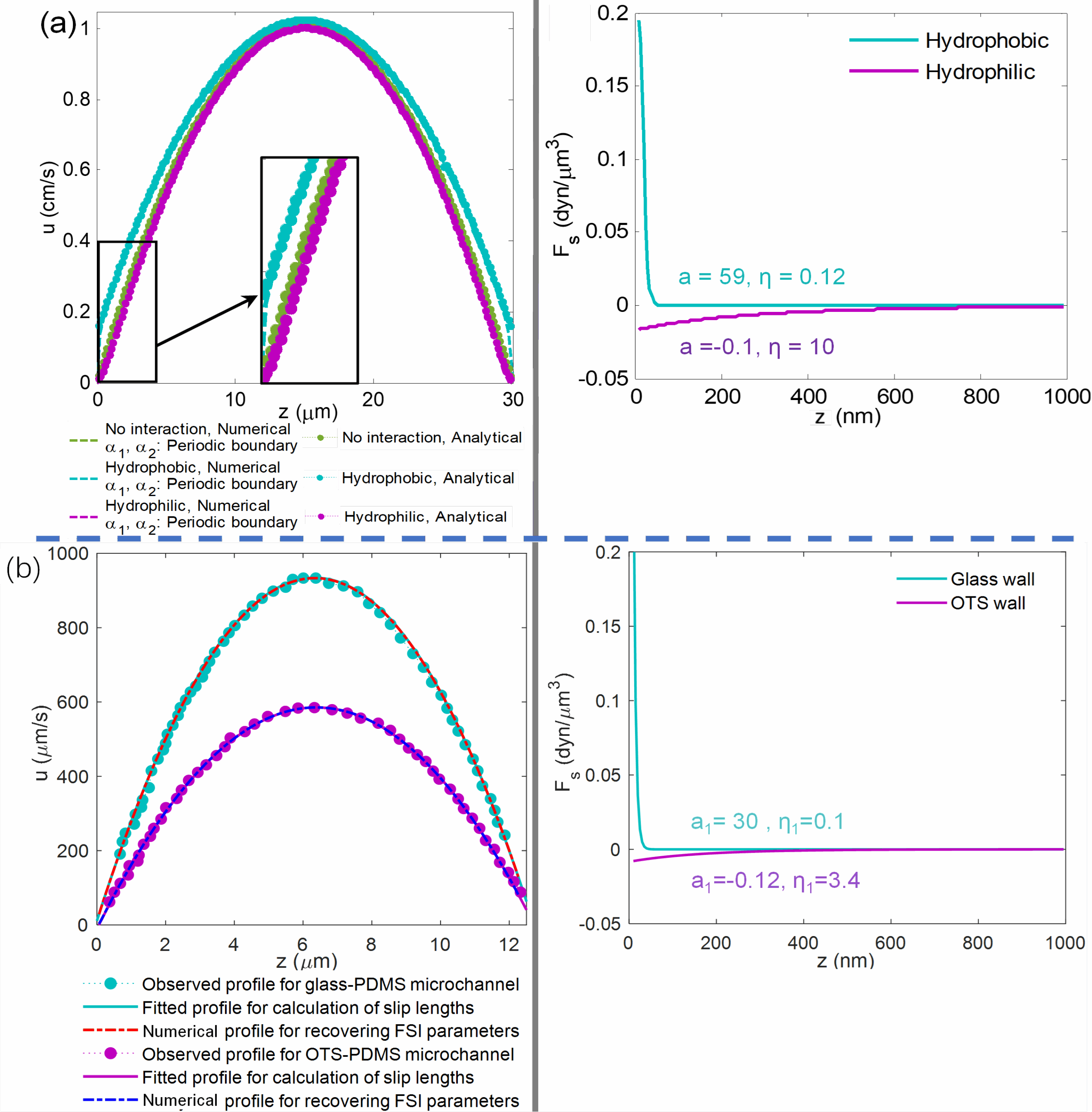
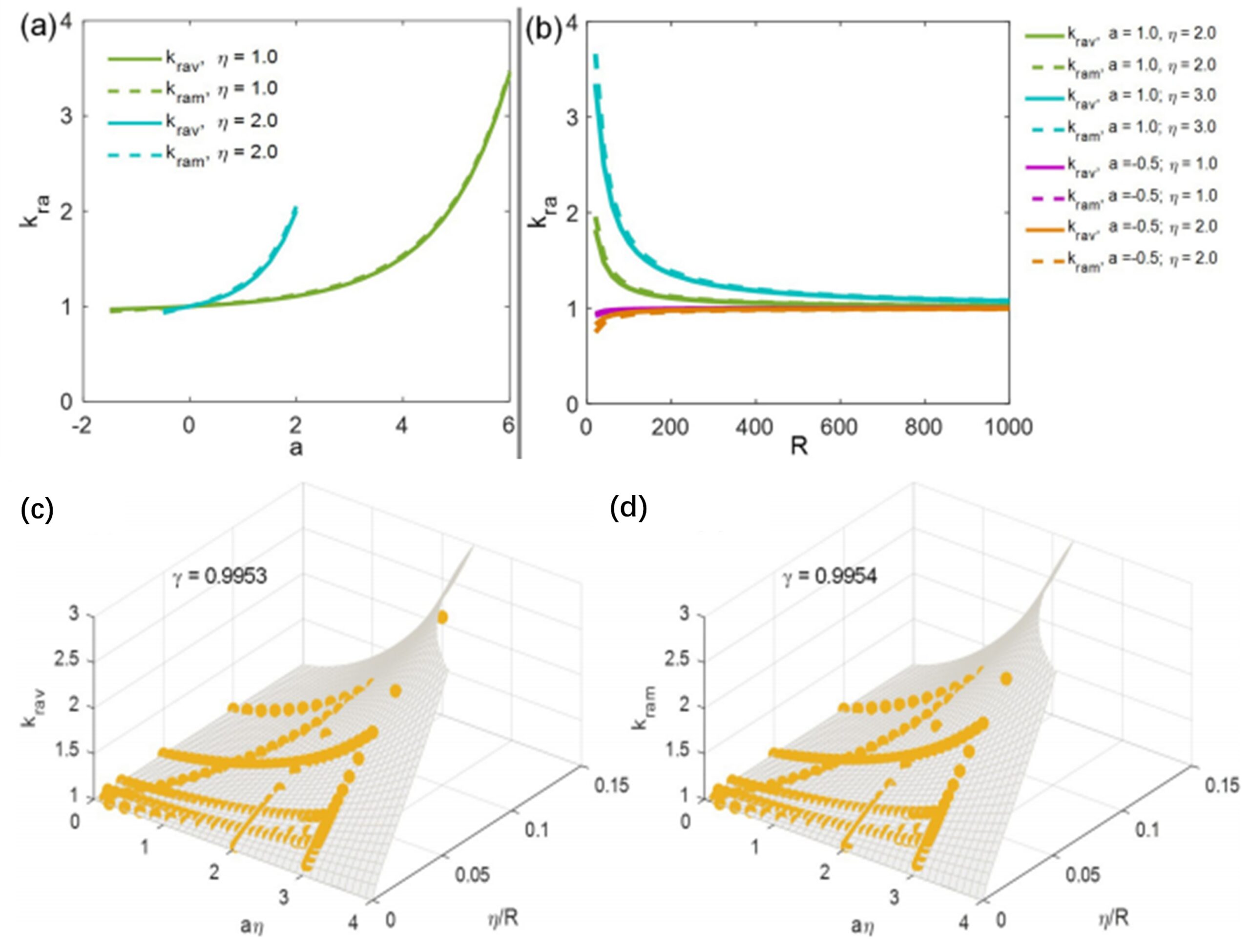
(a2)根据密度分布解析解,推导出薄膜水和自由水的密度比,并依据该密度比的实验观测值,给出了粘附作用强度与衰减长度两个介观物理参数的取值范围;根据流量提高比和滑移长度的解析解,验证了流量提高比和滑移长度的宏观本构关系式;根据流量提高比关于通道间隙宽度的解析解,证明了流量提高比随着通道间隙宽度的减小而增大(图2b),即滑移现象对纳米尺度或微米尺度下(低渗透性多孔介质,比如油页岩、高岭土)的液体流动有巨大的影响;根据上述解析解,推导出平行平板微通道滑移流系统的两个无量纲数,分别表示粘附作用强度(图2a)和作用距离,通过拟合给出了流量提高比关于两个无量纲数的本构关系式;拟合结果还发现,两个无量纲参数可以整合为一个无量纲参数,用来表征该系统的粘附作用强度或者滑移流程度(图2c,图2d)。
(b1)推导出了多相格子Boltzmann方法框架下平行平板通道内考虑流-固吸附作用的状态方程,发现了润湿角余弦值、薄膜水厚度和薄膜水与自由水的密度比均与流-固吸附作用强度呈现非线性增加的趋势,验证并率定了(考虑水气界面曲率和薄膜水厚度的)杨-拉普拉斯扩展方程;排水过程中,在到达残余含水量之前(毛细水与薄膜水共存),毛细水占据更狭窄的孔隙,薄膜水占据更多的颗粒表面积,且薄膜水厚度保持不变,并不是随着水-气界面曲率变化(图3)(传统土壤持水理论认为,多孔介质内薄膜水吸力等于毛细水吸力,Lebeau et al., 2010; Peters, 2013,进而薄膜水厚度会不断增加);薄膜水吸力远大于毛细水吸力,贡献了低渗透性多孔介质的超高基质吸力(图3)。
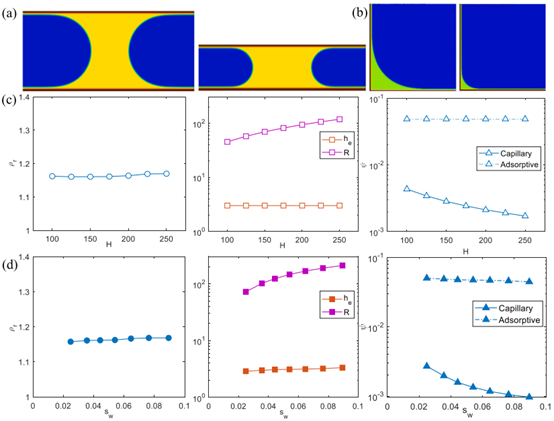
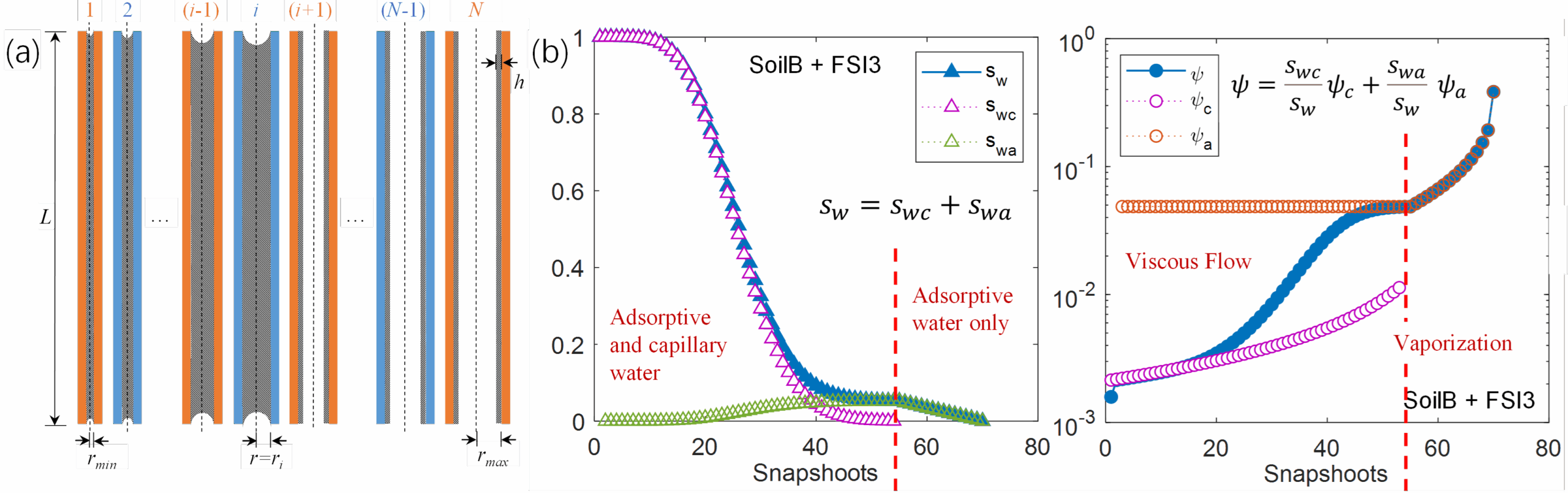
(b2)薄膜水的存在导致基质吸力值增大(流-固吸附作用贡献了楔裂压)和持水曲线形状变得更加陡峭(流-固吸附作用改变了有效孔隙分布);该发现更新了传统土壤持水理论中的假设;在低于残余含水量之后(毛细桥断裂、水分以薄膜水和角区毛细水为主),薄膜水厚度由于蒸发作用不断减小(图4)。根据上述排水过程的物理机制,可以求解毛细水和薄膜水对于基质吸力和总含水量的各自贡献。结合毛管束理论提出新的多孔介质基质吸力升维计算方案,结果与实验测得的黏土基质吸力曲线形状呈现定性的一致。
参考文献:
- Z. Li, J. Li, G. Yan, S. Galindo-Torres, A. Scheuermann, L. Li. (2021). Mesoscopic model framework for liquid slip in a confined parallel-plate flow channel. Physical Review Fluid, 6, 034203. https://doi.org/10.1103/PhysRevFluids.6.034203.
- Z. Li, Z. Yang, S. Galindo-Torres, L. Li. (2025). Lattice Boltzmann modelling of capillarity, adsorption and fluid retention in simple geometries: Do capillary and film water have equal matric suction or not? Advances in Water Resources, 199, 104950. https://doi.org/10.1016/j.advwatres.2025.104950.
- Baudry, E. Charlaix, A. Tonck, D. Mazuyer, Experimental evidence for a large slip effect at a nonwetting fluid-solid interface, Langmuir 17, 5232 (2001).
- S.J. Craig, C. Neto, D.R.M. Williams, Shear-Dependent Boundary Slip in an Aqueous Newtonian Liquid, Phys. Rev. Lett. 87, 54504 (2001).
- I. Vinogradova, Implications of hydrophobic slippage for the dynamic measurements of hydrophobic forces, Langmuir 14, 2827 (1998).
- I. Vinogradova, Slippage of water over hydrophobic surfaces, Int. J. Miner. Process. 56, 31 (1999).
- C. Tretheway, C.D. Meinhart, Apparent fluid slip at hydrophobic microchannel walls, Phys. Fluids 14, L9 (2002).
- Joseph, P. Tabeling, Direct measurement of the apparent slip length, Phys. Rev. E 71, 035303 (2005).
- Watanabe, K., Udagawa, Y., & Udagawa, H. (1999). Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. Journal of Fluid Mechanics, 381, 225-238.
- Churaev, N. V., Sobolev, V. D., & Somov, A. N. (1984). Slippage of liquids over lyophobic solid surfaces. Journal of Colloid and Interface Science, 97(2), 574-581.
- Lebeau, M., & Konrad, J. M. (2010). A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 46(12).
- Peters, A. (2013). Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resources Research, 49(10), 6765-6780.

